Understanding Diffusion Models Through Antithetic Noise

Introduction

Diffusion models have revolutionized generative AI by learning to transform random Gaussian noise into high-quality images, audio, and video. While much of the research has focused on architectural advances or accelerated sampling techniques, in this blog, we turn our attention to a third, often-overlooked ingredient: the properties of the initial Gaussian noise itself.

We present a systematic study of a universal phenomenon: antithetic noise pairs (initial noise with its negation ) consistently produces strongly negatively correlated sample trajectories across a wide range of diffusion models.

This property enables training-free enhancements, leading to increased image diversity and sharper uncertainty quantification, while achieving up to 100× computational savings in estimating downstream statistics.

Antithetic Noise Construction

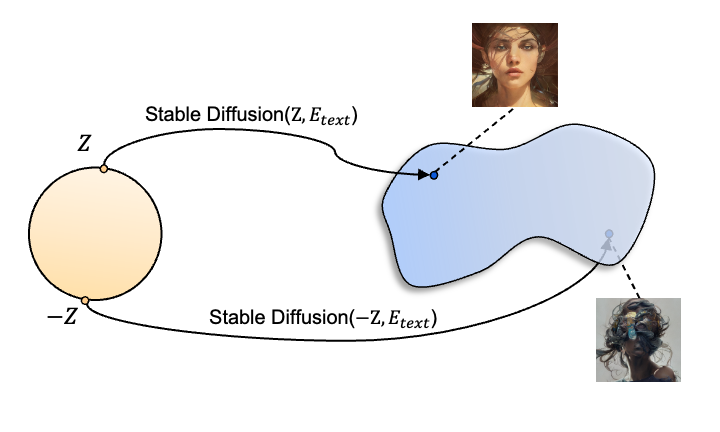
Antithetic Sampling Diagram

Figure 1: Conceptual illustration of antithetic noise in diffusion models. Starting from antipodal points in noise space z and -z, diffusion models map these to distant regions of the data manifold, producing negatively correlated but high-quality samples.

We begin by formalizing the core process of diffusion-based generation: sampling an initial noise vector $z \sim \mathcal{N}(0, I)$ and gradually denoising it through a given diffusion model’s mapping, denoted as $\text{DM}$ .

As shown in Figure 1, instead of drawing a single noise vector , we pair it with its negation . Formally, for each , we run two parallel diffusion processes that share the same magnitude but have opposite directions. This yields two output samples:

$\text{DM}(z)$ from
$\text{DM}(-z)$ from

Since both initial noises are drawn from the same marginal distribution, the generation quality of $\text{DM}(z)$ and $\text{DM}(-z)$ is preserved.

Moreover, if we imagine a scenario where the score network is exactly linear, feeding it with and would yield a perfect negative correlation (i.e., correlation of −1) between $\text{DM}(z)$ and $\text{DM}(-z)$ . Motivated by this intuition, we proceed to analyze the pixel-wise Pearson correlation coefficients of the generated sample pairs.

The Universal Negative Correlation Phenomenon

We observed that: initializing a diffusion model with paired noise vectors consistently yields strongly negatively correlated outputs, regardless of the sampling method or model type.

Experiment 1: Pixel-wise Correlation Analysis

To quantify the effect of antithetic noise initialization, we measured the pixel-wise Pearson correlation coefficients between pairs of generated images under two sampling schemes across four benchmark settings: CIFAR-10, CelebA-HQ, LSUN-Church, and text-conditioned Stable Diffusion.

We compared two pairing strategies:

Positive/Negative (PN): A single Gaussian noise vector is paired with its negation .
Random/Random (RR): Two independent Gaussian noise vectors and are sampled.

In each setting, we generated hundreds of image pairs and computed the Pearson correlation between the pixel values of each pair. The results show a consistent pattern:

PN pairs exhibit strong negative correlations, with mean values ranging from –0.33 to –0.76 across datasets.
RR pairs, by contrast, show mildly positive correlations, with mean values between +0.05 and +0.24.

This contrast highlights how antithetic noise causes outputs to diverge in a structured, opposing manner, while independent noise yields more loosely related results due to shared model priors.

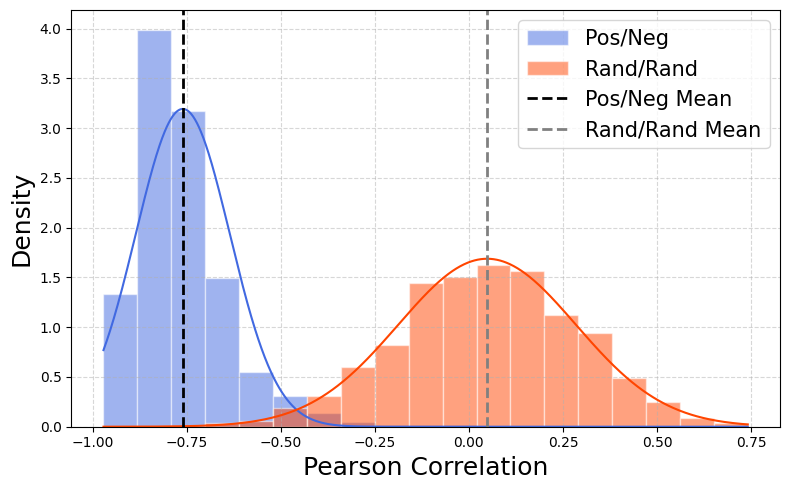
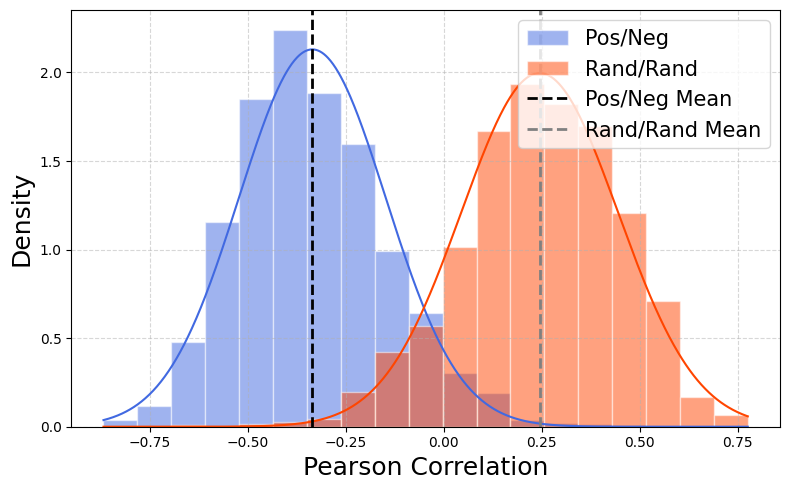
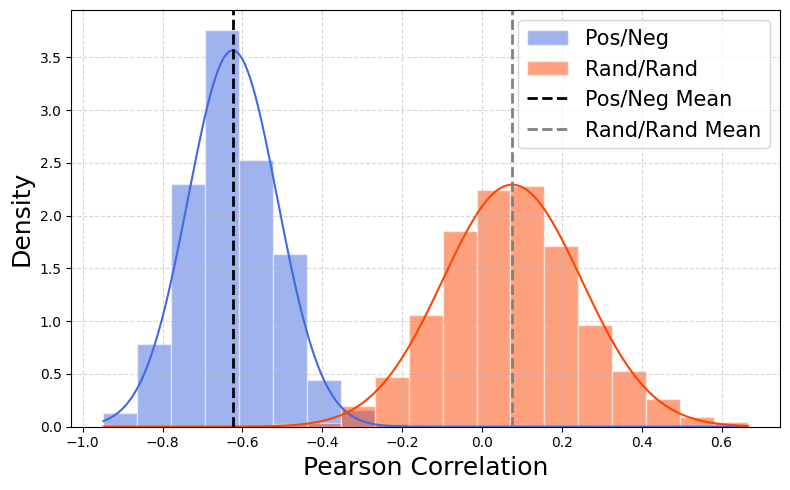
CIFAR-10 DDIM CelebA DDIM LSUN-Church DDIM

(a) CIFAR-10 (DDIM) (b) CelebA-HQ (DDIM) (c) LSUN-Church (DDIM)

Figure 2: Pearson correlation histograms for image pairs generated using antithetic noise (PN, blue) and independent noise (RR, orange) with DDIM. Dashed lines indicate mean correlation values. PN distributions are sharply left-skewed, indicating strong negative correlation.

What About DDPM?

While our initial experiments focused on DDIM, we extended the analysis to DDPM, which introduces additional stochasticity during sampling. Unlike DDIM, where the trajectory is fully deterministic once the initial noise is fixed, DDPM adds fresh Gaussian noise at each denoising step.

As a result, to preserve the antithetic structure in DDPM, we must not only negate the initial noise , but also negate the injected noise at every sampling step.

Despite this added complexity, the results follow a familiar pattern: strong negative correlations for antithetic pairs (PN), and weak positive ones for random pairs (RR).

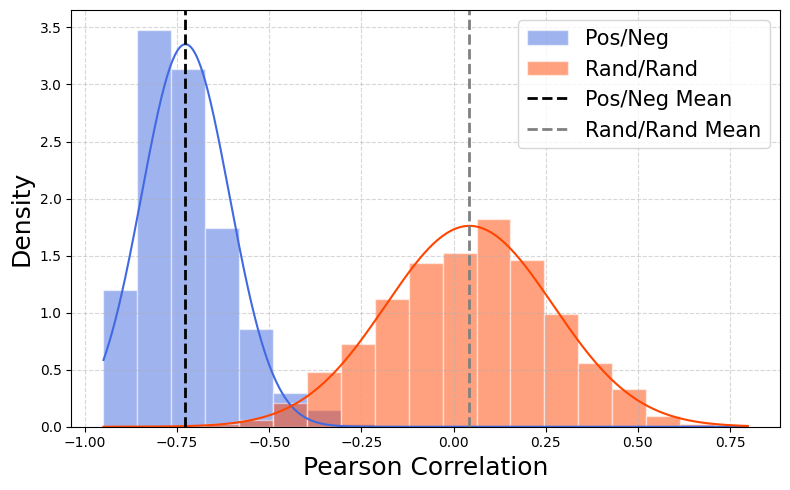
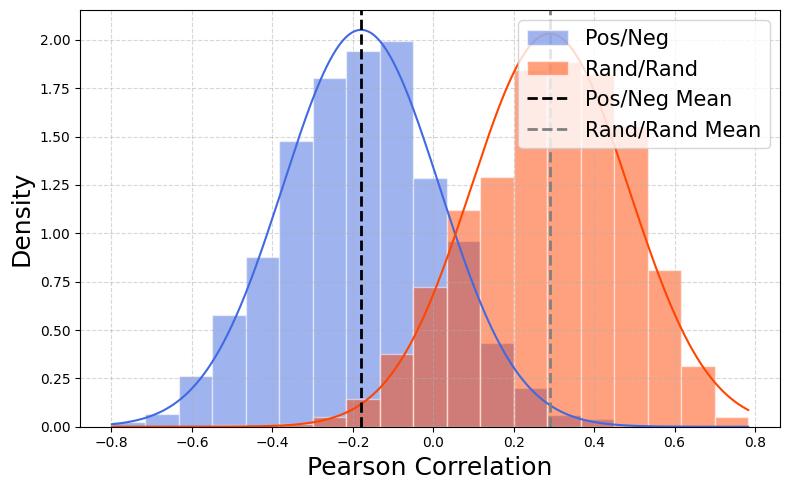
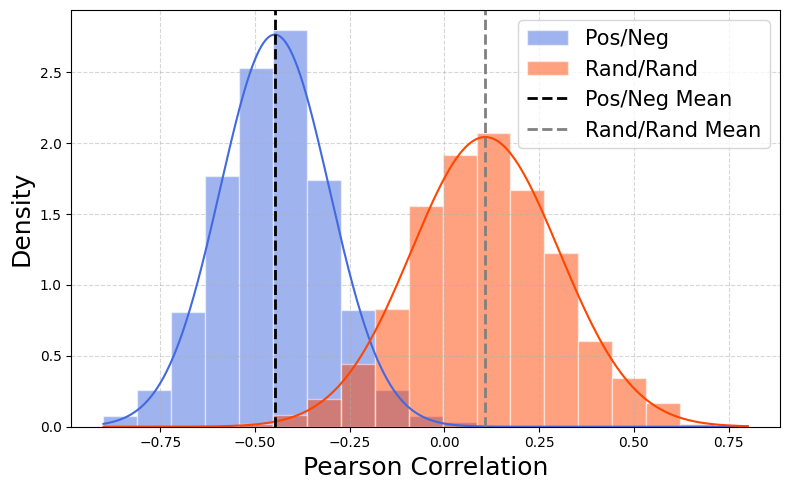
CIFAR-10 DDPM CelebA DDPM Church DDPM

(a) CIFAR-10 (DDPM) (b) CelebA-HQ (DDPM) (c) LSUN-Church (DDPM)

Figure 3: Pearson correlation histograms for PN and RR pairs across three datasets using DDPM. PN pairs (blue) remain negatively correlated, even under stochastic sampling.

Experiment 2: Temporal Correlations

Following the reuslt as antithetic noise pairs consistently produce negatively correlated samples, we then asked: how does this correlation evolve over time during sampling? Since diffusion models generate data step-by-step over iterations, understanding how antithetic structure behaves across these steps could offer clues into why the negative correlation persists so robustly.

To investigate this, we tracked the correlation between intermediate states and their associated predicted noise values $\epsilon_\theta^{(t)}(x)$ from the pre-trained model over using antithetic pairs (z, -z) .

As shown in Figure 3:

At the initial timestep (Step 50), the correlation between and is nearly –1, as expected—they’re direct opposites.
As denoising progresses, the correlation remains strongly negative, only slightly increasing toward the final few steps.
This pattern holds not only for the data trajectories (solid lines) but also for the predicted noise estimates $\epsilon_\theta^{(t)}(x)$ (dashed lines).

This near-perfect inverse relationship throughout the denoising process suggests that the learned score network $\epsilon_\theta$ may be enforcing a kind of functional symmetry.

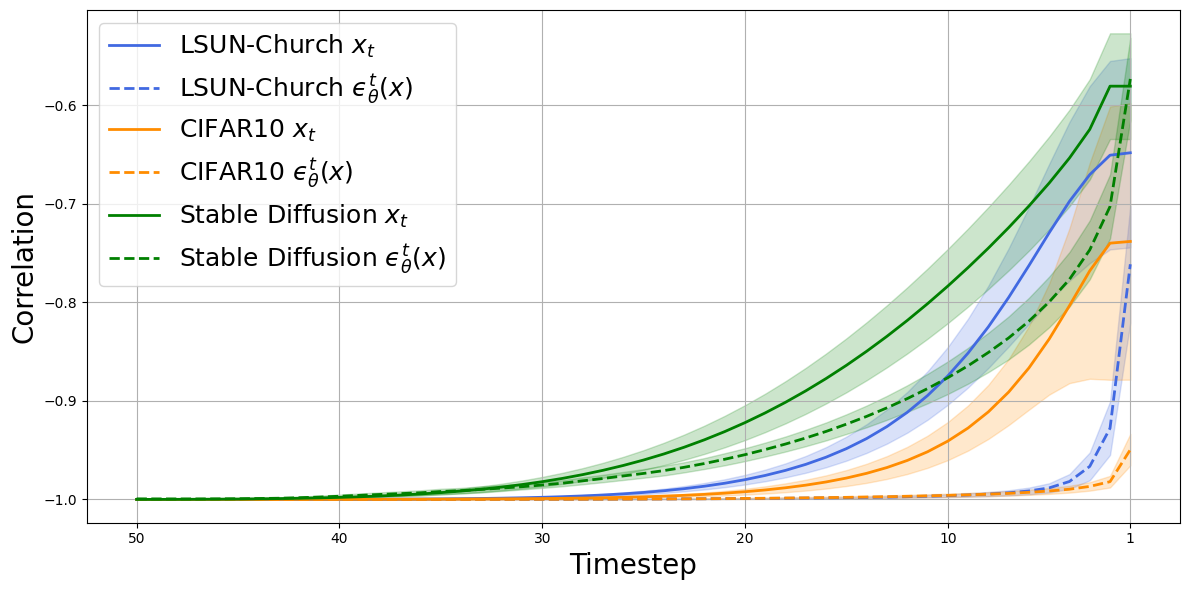
Temporal Correlation Plot

Figure 3: Correlation of $x_t$ (solid) and $epsilon$ (dashed) between antithetic (PN) pairs across time steps. Step 50 is the initial noise; Step 0 is the final output. Negative correlation persists across the entire diffusion process.

The Asymmetry Conjecture

To explain this behavior, we propose the asymmetry conjecture: diffusion models’ learned score functions $\epsilon_\theta^{(t)}(x)$ are approximately affine antisymmetric at each timestep . Formally,

$\epsilon_\theta^{(t)}(x) + \epsilon_\theta^{(t)}(-x) = 2c$

for some constant that depends on .

This implies the model treats noise and its negation symmetrically up to a shift, meaning that feeding the model and yields outputs that mirror each other around a consistent center throughout the sampling process.

Links to Negative Correlation

This mathematical property combined with DDIM update rule directly can explain the perfect negative correlation:

Since DDIM update rule can be expressed as a linear combination between the current state and the score network’s output:

$F_t(x) = a_t x + b_t \epsilon_\theta^{(t)}(x).$

Under the asymmetry conjecture, we find:

$F_t(-x) \approx -F_t(x) + 2b_t c_t,$

which shows that each DDIM update step preserves the antisymmetric structure which is the strong negative correlation between paired antithetic samples from initialization to the final generated output.

Empirical Validation

To empirically test this conjecture, we used a pretrained CIFAR-10 score network. At selected timesteps $t = 1, 3, 5, \dots, 19$ , we sampled $x \sim \mathcal{N}(0, I)$ , evaluated the first coordinate of $\epsilon_\theta^{(t)}(c x)$ as varied from to (interpolating from to ), and visualized the results.

As shown below, each curve demonstrates a near-perfect mirror symmetry, confirming that the score network behaves in an affine antisymmetric manner throughout the diffusion process. At larger (closer to pure noise), the curves become almost perfectly linear, while at smaller (closer to the image), mild non-linear oscillations appear but still maintain approximate symmetry around a center c_t .

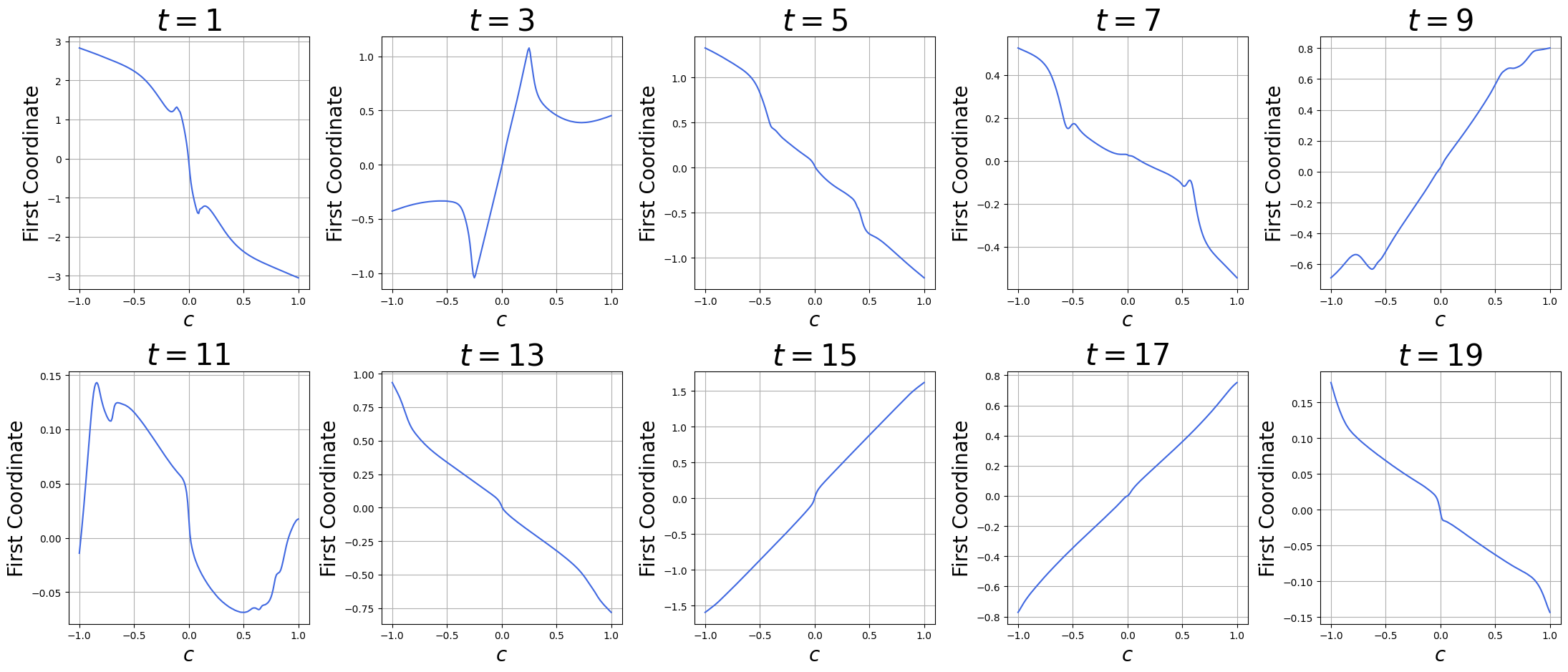
First-coordinate output symmetry test for CIFAR-10 score network under DDIM

Figure 4: First-coordinate output of the pretrained CIFAR-10 score network as a function of the interpolation scalar.

Enhancing Diversity in Generative Models

The negative correlation property enables a simple yet effective method for increasing image diversity. By using antithetic noise pairs instead of independent random samples, the generated images are "pushed" toward more distant regions of the data manifold. Notably, this aligns seamlessly with the workflows of many diffusion-based generative tools (such as DALL·E and Midjourney), which already generate multiple images from a single prompt to let users select their favorite.

We observe that models generate significantly more diverse sample (as shown in Table 1), and this enhancement comes "for free" - requiring no additional training, model modifications, or computational overhead beyond generating one extra sample.

Metric	CIFAR-10	LSUN-Church	CelebA-HQ	DrawBench	Pick-a-Pic
SSIM (%)	86.1	34.0	32.9	21.5	19.0
LPIPS (%)	8.3	4.2	18.1	4.8	5.4

Table 1: Average percentage improvement of PN over RR pairs.

Improving Uncertainty Quantification

Beyond diversity, the strong negative correlation induced by antithetic noise also offers a clear practical advantage in uncertainty quantification during generation and inference tasks.

To evaluate this, we computed 95% confidence intervals (CIs) on statistics using the following estimators,

MC (Monte Carlo)
- generate independent Gaussian noise samples, compute the statistic of interest for each generated output, and take the average.
AMC (Antithetic Monte Carlo)
- generate antithetic noise pairs . Each pair produces two negatively correlated samples, and their statistics are averaged.
QMC (Quasi-Monte Carlo)
- generate $N = M \times R$ samples by using low-discrepancy Sobol’ sequences to generate a point set of size in the noise space and over independent replicates for randomization.

Then, we measure relative efficiency as $(\text{CI}_{\text{MC}} / \text{CI}_A)^2$ to quantify how many fewer samples the alternative estimator needs to match MC’s CI width.

Simple Pixel-Wise Statistics

We evaluate AMC and QMC across:

Unconditional models (CIFAR-10, CelebA-HQ, LSUN-Church),
Stable Diffusion (text-to-image generation).

Metrics evaluated include brightness, pixel mean, contrast, and centroid location and the result is shown below.

Dataset		Brightness	Pixel Mean	Contrast	Centroid
Stable Diff.	MC	5.45	5.59	2.18	4.03
	QMC	1.35 (16.13)	1.42 (15.23)	1.03 (4.46)	1.88 (4.54)
	AMC	1.26 (18.83)	1.41 (15.84)	0.89 (6.25)	1.62 (6.15)
CIFAR10	MC	2.00	2.04	1.08	0.11
	QMC	0.35 (32.05)	0.39 (26.94)	0.22 (23.43)	0.04 (7.35)
	AMC	0.35 (32.66)	0.39 (27.12)	0.23 (22.05)	0.04 (6.96)
CelebA	MC	1.82	1.76	0.60	0.60
	AMC	0.26 (50.16)	0.31 (33.15)	0.19 (10.18)	0.20 (8.27)
Church	MC	1.67	1.67	1.02	0.70
	AMC	0.14 (136.37)	0.16 (106.79)	0.20 (27.16)	0.40 (3.14)

Table 2: Confidence interval (CI) length reductions and efficiency gains using Antithetic Monte Carlo (AMC) over standard Monte Carlo (MC) across tasks and datasets.

Inverse Problems: Bayesian Uncertainty

We further applied antithetic sampling to Bayesian inverse problems using diffusion posterior sampling (DPS) for inpainting tasks on CelebA-HQ:

50 DPS reconstructions were generated using PN and RR noise pairs.
AMC reduced CI lengths while preserving consistency in L1 and PSNR estimates.
Efficiency gains of 1.5x to 1.7x were observed without compromising reconstruction quality.

Conclusion

We explored a universal structural property in diffusion models: antithetic noise initialization consistently induces strong negative correlation throughout the generation process. We connected this to the approximate affine antisymmetry of the learned score network, providing a clear, theory-backed explanation.

Our findings translate into practical, zero-cost tools:

Enhances diversity in both unconditional and text-conditioned generation,
Improves uncertainty quantification by reducing variance in Monte Carlo estimators,
Requires no architectural changes or additional training, integrating seamlessly with existing diffusion pipelines.

By focusing on fundamental, universal properties rather than model-specific tricks, this work contributes to the theoretical foundations of diffusion models while providing practical methods for real-world workflows in generative AI, scientific modeling, and beyond.